Pharmacoepidemiology
Epidemiology concerns itself with the health of populations, and more specifically seeks to understand - and hence to influence - the relationships between exposure factors like smoking, diet, poverty and health outcomes like cancer, obesity, and life expectancy. Pharmacoepidemiology is the sub-discipline of epidemiology that deals with the effects of pharmaceutical drugs in populations.
Of particular importance are the adverse events associated with drugs. For example, aspirin taken at low doses over a long period reduces the risk of stroke - but may increase the risk of developing a stomach ulcer. Likewise, the measles vaccines in current use protect 95% of vaccinated children from measles (and indirectly protect unvaccinated children as well), but may very occasionally cause a child to have a convulsion.
Describing and quantifying these adverse effects accurately is a difficult statistical problem requiring suitable statistical methods. Several researchers within the Open University Medical Statistics Research Group work on developing and improving statistical methods in pharmacoepidemioloy.
The self-controlled case series method
Paddy Farrington and Heather Whitaker work on the self-controlled case series (SCCS) method. This is an economical way to analyse data from large databases that avoids some of the potential biases of traditional approaches in pharmacoepidemiology.
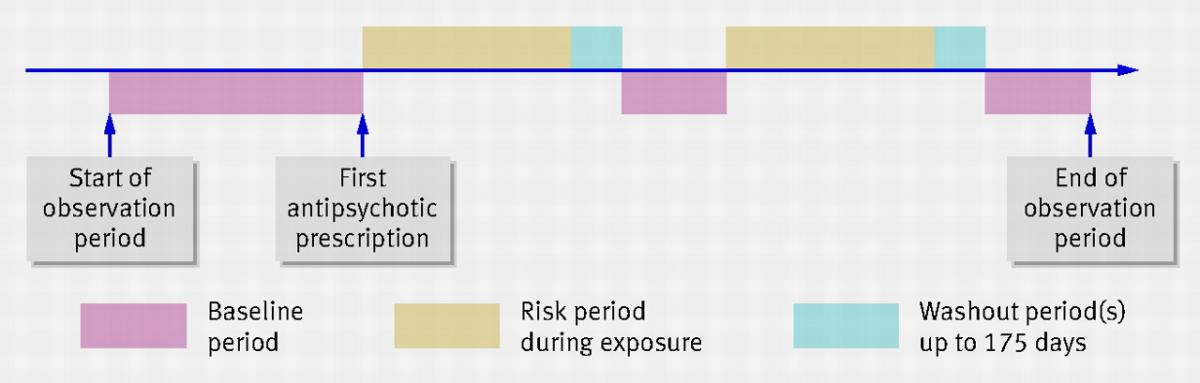
A diagrammatic example of one particular SCCS study (source: BMJ 2008;337:a1227).
Confounders
One big problem in pharmacoepidemiology is how to avoid the biases that may arise in estimating the strength of association between a drug and an adverse event, because the data available are not usually obtained under experimental conditions. This makes it tricky to choose suitable comparison groups who do not take the drug.
For example, suppose that we are interested in the impact of antidepressants on hip fracture in the elderly. If antidepressants tend to be given to people who, for whatever reason, are more likely than average to experience falls, then antidepressants will appear to be positively associated with hip fracture when compared to elderly people not on antidepressants. Similarly, if antidepressants tend to be prescribed to people who are less at risk of a fall, then they will appear to be negatively associated with hip fractures. The problem is that we usually can't adequately quantify "being at risk of a fall" to take account of this factor in the analysis.
The variable describing the underlying risk of a fall for each individual in the previous paragraph is called a confounder. And confounding is the impact of confounders on the analysis. Confounding is the bugbear of epidemiology. One way round it, popularised by Sir Austin Bradford Hill, is to allocate individuals randomly to take drug or not, thus evening out any differences between individuals. This is now the accepted way in which new drugs are evaluated. However, such randomised trials cannot be used for very rare adverse events, or when a drug has already been shown to have a benefit, since it would be unethical to withhold the drug from someone who needs it.

Sir Austin Bradford Hill (1897-1991), who popularised the use of randomised controlled clinical trials in evaluating pharmaceutical drugs. Random allocation removes the problem of confounding.
The self-controlled case series method
Existing statistical methods in pharmacoepidemiology can handle confounders, provided that we know what these confounders are and have measured them accurately. However, often the confounders are unknown, or unmeasured, or imperfectly measured. The self-controlled case series (or SCCS) method has the big advantage of also removing the effect of all confounding variables, known and unknown, which do not vary over time (confounders that vary over time must still be measured).
The basic idea of the SCCS method is that each individual is compared to her or himself at different points in time, so that the effect of any time-invariant confounder is removed. An added bonus is that only individuals who experience the health event of interest (for example, a hip fracture) need be included in the study. This can greatly simplify the analysis of rare events: for example, the data need only be checked for those individuals with the event.
Applications of the SCCS method
The SCCS method, first proposed by Paddy Farrington in 1995, has become increasingly popular over the past decade. Heather Whitaker has played a key role in making the SCCS method available to researchers, by programming it in standard packages. The SCCS method is particularly convenient for use in conjunction with the large electronic databases that are increasingly used for administrative purposes within the health system in the UK and elsewhere. Such databases tend not to include many details of potential confounders, so it is particularly important to use statistical methods that are to some extent robust to confounding.
Ongoing research at the OU
The SCCS method, however, requires several additional assumptions which may or may not be verified in practice. Much of the research on the SCCS method undertaken at the Open University over the past decade has sought to weaken these assumptions. Thus, several versions of the SCCS method are now available. Currently we are undertaking further work to increase the versatility and flexibility of the method, and to make these new (and unfortunately more complicated) extensions of the SCCS method more accessible to medical researchers who might wish to use them.
What is the SCCS?
The self-controlled case series method, a statistical method for evaluating the strength of association between a drug (or other exposure factor) and a health event.
How is it used?
It is used in pharmacoepidemiology, particularly in conjunction with computerised databases of health records.
Why is it useful?
The method is self-matched, and hence all time-invariant confounders are controlled. It is also economical in that it uses only individuals with the event of interest.

