You are here
- Home
- Research
- Research groups
- Applied Mathematics and Theoretical Physics
- Statistical Physics
Statistical Physics
Many physical and biological systems contain a large number of particles which have complicated interactions. The use of statistical methods to describe such apparently intractable problems has been one of the greatest triumphs of theoretical physics. In recent years, the emphasis has shifted towards systems which are far from equilibrium.
Phase transition and critical phenomena
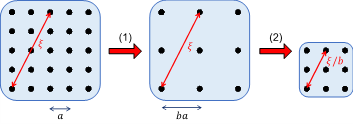
Our research focuses on understanding phase transitions and critical phenomena in various physical and biological systems. During phase transition and at critical point, the system exhibits scale invariance, which means that the system looks the same when viewed at different length scales. This property can then be exploited using theoretical tools such as renormalization group (see figure below).
Living and active matter
We are interested in mathematical and statistical modelling of biological systems, ranging from small scales (such as cell migration and tissues) to large scales (such as population dynamics). Some of the work in our group include: applying non-equilibrium statistical physics to tissue dynamics, finite element modelling of cochlear implant, and modelling infectious disease dynamics.

Stochastic and chaotic systems
We study stochastic and chaotic processes in physical, biological and environmental systems using large deviation theory, bifurcation analysis, random dynamical systems and spin systems, as well as a wide range of statistics and machine learning methods. An example of a stochastic model for the motion of particles in a turbulent fluid flow is shown in the image below.

Econophysics
We use tools and concepts from statistical physics to understand the dynamics of stock markets, in particular, the emergence of macroscopic phenomena such as bubbles and crashes. For instance, during an economic bubble, the stock market price displays a log-periodic behaviour, reminiscent of a fractal.

Statistical Physics Group
Central Academics
Jim Hague
Ben Mestel
Marc Pradas
Elsen Tjhung
Paul Upton
Staff Tutors
Vicki Brown
Colette Christiansen
Andrew Neate

