Geometry and Dynamics
The Geometry and Dynamics Group researches applications of geometry within dynamics.
SL2-tilings
This topic concerns the study of SL2-tilings using the Farey graph, which is a graph that arises from a tessellation of the hyperbolic plane by ideal triangles. A sample SL2-tiling and a copy of the Farey graph embedded in the disc model of the hyperbolic plane are shown below. This research is funded by the EPSRC grant EP/W002817/1. 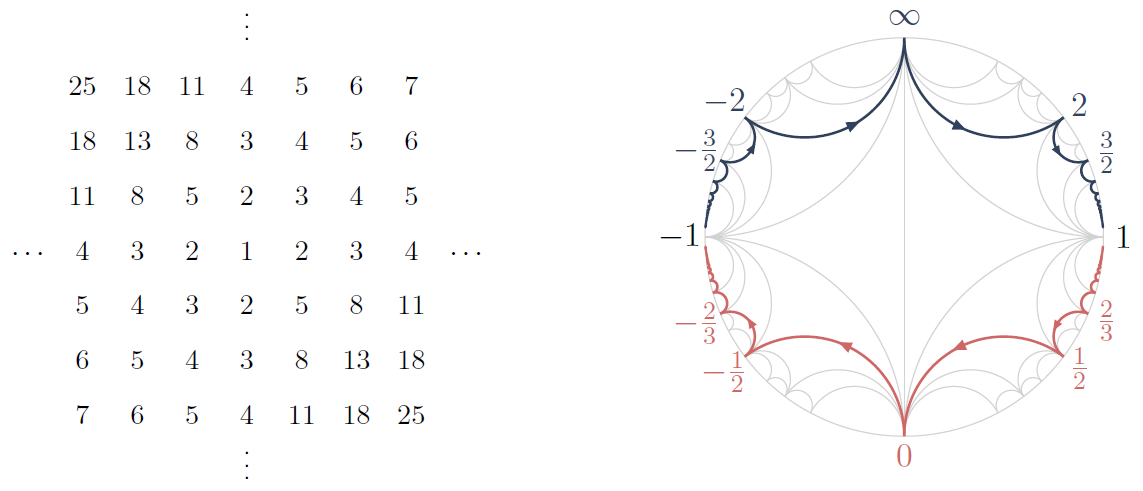
Geometry of numbers
Here we consider applications of geometry to number theory and dynamics, with particular focus on theory of continued fractions. Geometric tools include integer lattice geometry and the Farey graph.
Semigroups of isometries of the hyperbolic plane
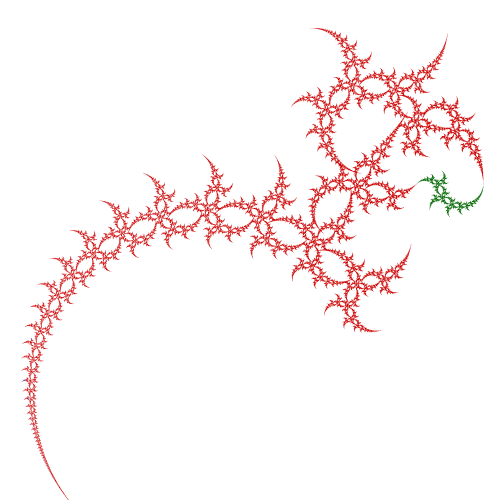
This topic is about the interaction between semigroup theory and dynamics for collections of hyperbolic isometries. Significant in this study are the forward and backward limit sets of semigroups of Möbius transformations, such as those shown in the figure below.
Geometry and Dynamics Group
Central Academics
Research Associates and Fellows
Research Students
Margaret Stanier
Andrei Zabolotskii

